function_function翻译成中文

function_function翻译成中文

       大家好，我是小编，今天我来给大家讲解一下关于function的问题。为了让大家更容易理解，我将这个问题进行了归纳整理，现在就一起来看看吧。

1.function 在表示 功能 之意时 是否可数额?

2.js中的function是什么意思

3.functional与function是什么意思

4.function是什么意思

5.function函数的用法

6.func是什么意思？

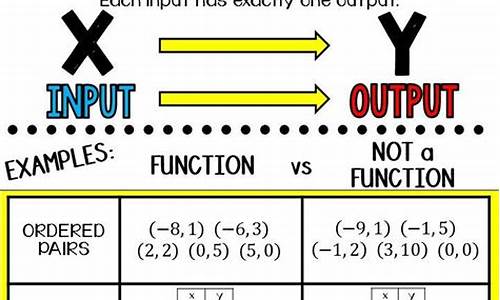
function 在表示 功能 之意时 是否可数额?

       function任何时候都是可数的。

       名词 n. [C]

       1.官能,功能,作用

       The teacher did not explain its grammatical function.

       老师没有解释它的语法功能。

       2.职务,职责

       What is his function on the committee?

       他在委员会里担任什么职务?

       3.盛大的集会(或宴会,宗教仪式)

       I attended many social functions while working abroad.

       我在国外工作期间出席了许多社交会。

       4.数函数

js中的function是什么意思

       在数学领域，函数是一种关系，这种关系使一个集合里的每一个元素对应到另一个（可能相同的）集合里的唯一元素。

       ----A variable so related to another that for each value assumed by one there is a value determined for the other.

       自变量，函数一个与他量有关联的变量，这一量中的任何一值都能在他量中找到对应的固定值。

       ----A rule of correspondence between two sets such that there is a unique element in the second set assigned to each element in the first set.

       函数两组元素一一对应的规则，第一组中的每个元素在第二组中只有唯一的对应量。

       函数的概念对于数学和数量学的每一个分支来说都是最基础的。

       ～‖函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数，记作 y=f(x).

       数集D称为函数的定义域，由函数对应法则或实际问题的要求来确定。相应的函数值的全体称为函数的值域，对应法则和定义域是函数的两个要素。

       functions

       数学中的一种对应关系，是从非空集合A到实数集B的对应。简单地说，甲随着乙变，甲就是乙的函数。精确地说，设X是一个非空集合，Y是非空数集，f是个对应法则， 若对X中的每个x，按对应法则f，使Y中存在唯一的一个元素y与之对应 ，就称对应法则f是X上的一个函数，记作y=f（x），称X为函数f（x）的定义域，集合{y|y=f（x），x∈X}为其值域（值域是Y的子集），x叫做自变量，y叫做因变量，习惯上也说y是x的函数。

       若先定义映射的概念，可以简单定义函数为：定义在非空数集之间的映射称为函数。

       例1：y=sinx X=[0，2π]，Y=[－1，1] ，它给出了一个函数关系。当然 ，把Y改为Y1=（a，b） ，a<b为任意实数，仍然是一个函数关系。

       其深度y与一岸边点 O到测量点的距离 x 之间的对应关系呈曲线，这代表一个函数，定义域为[0，b]。以上3例展示了函数的三种表示法：公式法， 表格法和图 像法。

       一般地，在一个变化过程中，如果有两个变量X与Y，并且对于X的每一个确定的值，Y都有为一得值与其对应，那么我们就说X是自变量，Y是X的函数。如果当X=A时Y=B，那么B叫做当自变量的值为A时的函数值。

       复合函数<IMG src=/it/u=937021061,4081051841&fm=0&gp=28.jpg name=pn0>

       有3个变量，y是u的函数，y=ψ（u），u是x的函数，u=f（x），往往能形成链：y通过中间变量u构成了x的函数：

       x→u→y，这要看定义域：设ψ的定义域为U。f的值域为U，当U*&Iacute;U时，称f与ψ 构成一个复合函数， 例如 y=lgsinx，x∈（0，π）。此时sinx>0 ，lgsinx有意义。但如若规定x∈（－π，0），此时sinx<0 ，lgsinx无意义，就成不了复合函数。 若能由函数方程F（x，y）=0 确定y为x的函数y=f（x），即F（x，f（x））≡0，就称y是x的隐函数。

       思考：隐函数是否为函数？因为在其变化的过程中并不满足“一对一”和“多对一” 设点（x1，x2，…，xn） ∈G&Iacute;Rn，U&Iacute;R1 ，若对每一点（x1，x2，…，xn）∈G，由某规则f有唯一的 u∈U与之对应：f：G→U，u=f（x1，x2，…，xn），则称f为一个n元函数，G为定义域，U为值域。

       基本初等函数及其图像幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。 y=ax（a>0 ，a≠1），定义成为（－∞，+∞），值域为（0 ，+∞），a>0 时是严格单调增加的函数（即当x2>x1时，） ，00）， 称a为底 ， 定义域为（0，+∞），值域为（－∞，+∞）。a>1 时是严格单调增加的，0<a<1时是严格单减的。不论a为何值，对数函数的图形均过点（1，0），对数函数与指数函数互为反函数。如图5。

       以10为底的对数称为常用对数 ，简记为lgx。在科学技术中普遍使用的是以e为底的对数，即自然对数，记作lnx。三角函数　见表2。

       正弦函数、余弦函数如图6，图7所示。反三角函数　见表3。双曲正、余弦如图8。双曲函数　双曲正弦（ex－e-x），双曲余弦?（ex+e-x），双曲正切（ex－e-x）/（ex+e-x） ，双曲余切（ex+e-x）/（ex－e-x）。

       补充

       在数学领域，函数是一种关系，这种关系使一个集合里的每一个元素对应到另一个（可能相同的）集合里的唯一元素（这只是一元函数f（x）=y的情况，请按英文原文把普遍定义给出，谢谢）。函数的概念对于数学和数量学的每一个分支来说都是最基础的。

       术语函数，映射，对应，变换通常都是同一个意思。二次函数定义和性质　一般地，自变量x和因变量y之间存在如下关系：

       y=ax^2+bx+c

       二次函数的三个通式：

       y=ax^2+bx+c （一般式，a≠0，对称轴：x=-b/（2a））

       y=a(x-h)^2+k （顶点式，a≠0，对称轴：x=h）

       y=a(x-x_1）（x-x_2） （交点式，a≠0，对称轴：x=|x_2-x_1|/2）

       说明：在一般式中，抛物线与y轴相交的点的纵坐标值为c，抛物线顶点为[-b/（2a），（4ac-b^2）/（4a)]

       在顶点式中，抛物线的顶点为（h,k）。

       在交点式中，抛物线与x轴交与（x_1,0），（x_2,0）两点。（前提是当y等于0时，Δ大于0，当Δ等于0时，x_1=x_2）

       （a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下。IaI还可以决定开口大小，IaI越大开口就越小，IaI越小开口就越大。）

       则称y为x的二次函数。

       二次函数表达式的右边通常为二次三项式。

       x是自变量，y是x的函数

       二次函数的三种表达式

       一般式：y=ax^2+bx+c（a，b，c为常数，a≠0）

       顶点式：y=a(x-h)^2+k [抛物线的顶点P（h，k）] 对于二次函数y=ax^2+bx+c 其顶点坐标为 (-b/2a，（4ac-b^2）/4a)</CA>

       交点式：y=a(x-x?)(x-x) [仅限于与x轴有交点A（x? ，0）和 B（x?，0）的抛物线]

       其中x1，2= -b±√b^2－4ac

       注：在3种形式的互相转化中，有如下关系：

       ______

       h=-b/2a k=（4ac-b^2）/4a x?,x?=(-b±√b^2-4ac)/2a

       二次函数的图像

       在<a href=#>；平面直角坐标系中作出二次函数y=x^2的图像，

       可以看出，二次函数的图像是一条抛物线。

       抛物线的性质

       ⒈抛物线是轴对称图形。对称轴为直线x = -b/2a。

       对称轴与抛物线唯一的交点为抛物线的顶点P。

       特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）

       ⒉抛物线有一个顶点P，坐标为P (-b/2a ，（4ac-b^2）/4a)

       当-b/2a=0时，P在y轴上；当Δ= b^2-4ac=0时，P在x轴上。

       ⒊二次项系数a决定抛物线的开口方向和大小。

       当a>0时，抛物线向上开口；当a<0时，抛物线向下开口。

       |a|越大，则抛物线的开口越小。

       ⒋一次项系数b和二次项系数a共同决定对称轴的位置。

       当a与b同号时（即ab>0），对称轴在y轴左；

       当a与b异号时（即ab<0），对称轴在y轴右。

       ⒌常数项c决定抛物线与y轴交点。

       抛物线与y轴交于（0，c）

       ⒍抛物线与x轴交点个数

       Δ= b^2-4ac>0时，抛物线与x轴有2个交点。

       Δ= b^2-4ac=0时，抛物线与x轴有1个交点。

       _______

       Δ= b^2-4ac<0时，抛物线与x轴没有交点。X的取值是虚数（x= -b±√b^2－4ac 的值的相反数，乘上虚数i，整个式子除以2a）

       当a>0时，函数在x= -b/2a处取得最小值f(-b/2a)=4ac-b^2/4a；在{x|x<-b/2a}上是减函数，在{x|x>-b/2a}上是增函数；抛物线的开口向上；函数的值域是{x|x≥4ac-b^2/4a}相反不变

       当b=0时，抛物线的对称轴是y轴，这时，函数是偶函数，解析式变形为y=ax^2+c(a≠0)

       二次函数与一元二次方程

       特别地，二次函数（以下称函数）y=ax^2+bx+c，

       当y=0时，二次函数为关于x的一元二次方程（以下称方程），

       即ax^2+bx+c=0

       此时，函数图像与x轴有无交点即方程有无实数根。

       函数与x轴交点的横坐标即为方程的根。

       1．二次函数y=ax^2，y=a(x-h)^2，y=a(x-h)^2 +k，y=ax^2+bx+c（各式中，a≠0）的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：

       解析式

       y=ax^2

       y=a(x-h)^2

       y=a(x-h)^2+k

       y=ax^2+bx+c

       顶点坐标

       （0，0)

       （h，0)

       （h，k)

       （-b/2a，sqrt[4ac-b^2]/4a)

       对 称 轴

       x=0

       x=h

       x=h

       x=-b/2a

       当h>0时，y=a(x-h)^2的图象可由抛物线y=ax^2向右平行移动h个单位得到，

       当h<0时，则向左平行移动|h|个单位得到．

       当h>0,k>0时，将抛物线y=ax^2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)^2 +k的图象；

       当h>0,k<0时，将抛物线y=ax^2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象；

       当h<0,k>0时，将抛物线向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)^2+k的图象；

       当h<0,k<0时，将抛物线向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象；

       因此，研究抛物线 y=ax^2+bx+c(a≠0）的图象，通过配方，将一般式化为y=a(x-h)^2+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了．这给画图象提供了方便．

       2．抛物线y=ax^2+bx+c(a≠0）的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=-b/2a，顶点坐标是（-b/2a，[4ac-b^2]/4a）．

       3．抛物线y=ax^2+bx+c(a≠0），若a>0，当x ≤ -b/2a时，y随x的增大而减小；当x ≥ -b/2a时，y随x的增大而增大．若a<0，当x ≤ -b/2a时，y随x的增大而增大；当x ≥ -b/2a时，y随x的增大而减小．

       4．抛物线y=ax^2+bx+c的图象与坐标轴的交点：

       ⑴图象与y轴一定相交，交点坐标为（0，c）；

       ⑵当△=b^2-4ac>0，图象与x轴交于两点A(x?，0）和B(x?，0），其中的x1,x2是一元二次方程ax^2+bx+c=0

       （a≠0）的两根．这两点间的距离AB=|x?-x?| 另外，抛物线上任何一对对称点的距离可以由|2×（-b/2a）－A |（A为其中一点）

       当△=0．图象与x轴只有一个交点；

       当△<0．图象与x轴没有交点．当a>0时，图象落在x轴的上方，x为任何实数时，都有y>0；当a<0时，图象落在x轴的下方，x为任何实数时，都有y<0．

       5．抛物线y=ax^2+bx+c的最值：如果a>0(a<0），则当x= -b/2a时，y最小（大）值=（4ac-b^2）/4a．

       顶点的横坐标，是取得最值时的自变量值，顶点的纵坐标，是最值的取值．

       6．用待定系数法求二次函数的解析式

       ⑴当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时，可设解析式为一般形式：

       y=ax^2+bx+c(a≠0）．

       ⑵当题给条件为已知图象的顶点坐标或对称轴时，可设解析式为顶点式：y=a(x-h)^2+k(a≠0）．

       ⑶当题给条件为已知图象与x轴的两个交点坐标时，可设解析式为两根式：y=a(x-x?)(x-x?)(a≠0）．

       7．二次函数知识很容易与其它知识综合应用，而形成较为复杂的综合题目。因此，以二次函数知识为主的综合性题目是中考的热点考题，往往以大题形式出现． 1．（北京西城区）抛物线y=x2-2x+1的对称轴是（　）

       （A）直线x=1　（B）直线x=-1　（C）直线x=2　（D）直线x=-2

       考点：二次函数y=ax2+bx+c的对称轴．

       评析：因为抛物线y=ax2+bx+c的对称轴方程是：y=-，将已知抛物线中的a=1，b=-2代入，求得x=1，故选项A正确．

       另一种方法：可将抛物线配方为y=a(x-h)2+k的形式，对称轴为x=h，已知抛物线可配方为y=(x-1）2，所以对称轴x=1，应选A．

       2．（北京东城区）有一个二次函数的图象，三位学生分别说出了它的一些特点：

       甲：对称轴是直线x=4；

       乙：与x轴两个交点的横坐标都是整数；

       丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3．

       请你写出满足上述全部特点的一个二次函数解析式：　．

       考点：二次函数y=ax2+bx+c的求法

       评析：设所求解析式为y=a(x-x1）（x-x2），且设x1<x2，则其图象与x轴两交点分别是A(x1，0），B(x2，0），与y轴交点坐标是（0，ax1x2）.

       ∵抛物线对称轴是直线x=4，

       ∴x2-4=4 - x1即：x1+ x2=8　①

       ∵S△ABC=3，∴（x2- x1）·|a x1 x2|= 3，

       即：x2- x1=　②

       ①②两式相加减，可得：x2=4+，x1=4-

       ∵x1，x2是整数，ax1x2也是整数，∴ax1x2是3的约数，共可取值为：±1，±3。

       当ax1x2=±1时，x2=7，x1=1，a=±

       当ax1x2=±3时，x2=5，x1=3，a=±

       因此，所求解析式为：y=±（x-7）（x-1）或y=±（x-5）（x-3）

       即：y=x2-x+1 或y=-x2+x-1 或y=x2-x+3 或y=-x2+x-3

       说明：本题中，只要填出一个解析式即可，也可用猜测验证法。例如：猜测与x轴交点为A（5，0），B（3，0）。再由题设条件求出a，看C是否整数。若是，则猜测得以验证，填上即可。

       5．（河北省）如图13-28所示，二次函数y=x2-4x+3的图象交x轴于A、B两点，交y轴于点C，则△ABC的面积为（　）

       A、6　B、4　C、3　D、1

       考点：二次函数y=ax2+bx+c的图象及性质的运用。

       评析：由函数图象可知C点坐标为（0，3），再由x2-4x+3=0可得x1=1，x2=3所以A、B两点之间的距离为2。那么△ABC的面积为3，故应选C。

       图13-28

       6．（安徽省）心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间满足函数关系：y=-0.1x2+2.6x+43(0<x<30）。y值越大，表示接受能力越强。

       ⑴x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？

       ⑵第10分时，学生的接受能力是什么？

       ⑶第几分时，学生的接受能力最强？

       考点：二次函数y=ax2+bx+c的性质。

       评析：将抛物线y=-0.1x2+2.6x+43变为顶点式为：y=-0.1(x-13）2+59.9，根据抛物线的性质可知开口向下，当x≤13 时，y随x的增大而增大，当x>13时，y随x的增大而减小。而该函数自变量的范围为：0≤x≤30，所以两个范围应为0≤x≤13； 13≤x≤30。将x=10代入，求函数值即可。由顶点解析式可知在第13分钟时接受能力为最强。解题过程如下：

       解：⑴y=-0.1x2+2.6x+43=-0.1(x-13）2+59.9

       所以，当0≤x≤13时，学生的接受能力逐步增强。

       当13<x≤30时，学生的接受能力逐步下降。

       ⑵当x=10时，y=-0.1（10-13）2+59.9=59。

       第10分时，学生的接受能力为59。

       ⑶x=13时，y取得最大值，

       所以，在第13分时，学生的接受能力最强。

       9．（河北省）某商店经销一种销售成本为每千克40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克．针对这种水产品的销售情况，请解答以下问题：

       ⑴当销售单价定为每千克55元时，计算月销售量和月销售利润；

       ⑵设销售单价为每千克x元，月销售利润为y元，求y与x的函数关系式（不必写出x的取值范围）；

       ⑶商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？

       解：⑴当销售单价定为每千克55元时，月销售量为：500–（55–50）×10=450（千克），所以月销售利润为

       ：（55–40）×450=6750（元）．

       ⑵当销售单价定为每千克x元时，月销售量为：[500–（x–50）×10]千克而每千克的销售利润是：（x–40）元，所以月销售利润为：

       y=(x–40）[500–（x–50）×10]=(x–40）（1000–10x)=–10x2+1400x–40000（元），

       ∴y与x的函数解析式为：y =–10x2+1400x–40000．

       ⑶要使月销售利润达到8000元，即y=8000，∴–10x2+1400x–40000=8000，

       即：x2–140x+4800=0，

       解得：x1=60，x2=80．

       当销售单价定为每千克60元时，月销售量为：500–（60–50）×10=400（千克），月销售成本为：

       40×400=16000（元）；

       当销售单价定为每千克80元时，月销售量为：500–（80–50）×10=200（千克），月销售单价成本为：

       40×200=8000（元）；

       由于8000<10000<16000，而月销售成本不能超过10000元，所以销售单价应定为每千克80元．

functional与function是什么意思

       在JavaScript中，function是一种用来封装可重用代码的方式。相当于一种特殊的对象，可以实现对代码的组织和封装。创建一个function后，就可以通过调用它来执行其中封装的代码，从而实现代码的重复使用。

       Function在JavaScript中具有许多特性。比如函数可以接收传入的参数，并在函数体内对其进行处理；函数可以返回一个结果值；函数也可以嵌套在其他函数内部，让代码更加简洁和可读。

       另外，Function还具有更高级的特性，如函数可以作为参数传递给其他函数，作为回调函数使用；函数也可以作为对象的方法使用，这样可以增加对象的行为等。

       使用function需要掌握函数的语法和基本规则，包括函数的定义、调用和执行等。在定义函数时，需要给它一个名称，并设置函数体内的代码。在调用函数时，可以传入函数的参数，然后函数就会按照预先定义好的方式对参数进行处理。执行函数时，函数体中封装的代码就会被执行。还需要注意函数的作用域、变量和闭包等问题，这些都是使用function时需要重点关注的方面。

function是什么意思

       你好

       functional

       [英][?f?k?nl][美][?f?k?n?l]

       adj.功能的; [数]函数的; 有多种用途的; 机能性;

       以上结果来自金山词霸

       例句:

       1.

       The controls remain straightforward, and the emphasis is on functional design rather thanaffordable luxury.

       它的操控仍然十分简洁，而且它的重点主要在于功能计设，而不是要打造成一款一般人负担得起的豪华车。

       function

       [英][?f?k?n][美][?f?k?n]

       n.功能，作用; 应变量，函数; 职务; 重大聚会;

       vi.有或起作用; 行使职责;

       第三人称单数：functions过去分词：functioned复数：functions现在进行时：functioning过去式：functioned

       以上结果来自金山词霸

       例句:

       1.

       Historically, designers have focused their attention on a product's form and function.

       在此之前，设计师们的重心是产品的外形和功能。

       -----------------------------------

       如有疑问欢迎追问！

       满意请点击右上方满意按钮

function函数的用法

       在java中，肯定有很多的用户对于function不陌生，而然知道它意思的少之又少，为了让更多的用户了解我们带来了详细介绍，不知道function是什么意思的可以看看。

       function是什么意思：

答：function的意思是一种关键字。

       一般表示子例程的一般性名词，在编程中可以表示返回值的子例程和语句。

       在语言中表示关键字，是很重要的存在，一般都是要获取函数参数信息。

       function相关介绍：

       1、function在java中表示对应对象方法，

       但是方法却不是对象，是不可以脱离对象的独立存在。

       2、而在JavaScript中，函数的实例是独立的对象，

       拥有属于自己的方法和属性，可以当参数传递。

func是什么意思？

       function函数的用法：function作为函数声明使用、类构造器使用、闭包使用、选择器使用、四种情况的混合应用、处理ajax返回的js脚本。

       function函数有六种用法：function函数最基本的作为一个本本分分的函数声明使用；function函数作为一个类构造器使用；function函数作为闭包使用；function函数可以作为选择器使用；function函数四种情况的混合应用；利用function函数处理ajax返回的js脚本。

       Function函数与Sub过程类似。但Function函数可以有返回值。可以使用参数。如果Function函数没有任何参数，则Function语句必须要包含空括号。Function函数通过函数名返回一个值。返回值的数据类型是Variant。

函数的特性

       1、有界性

       设函数f（x）在区间X上有定义，如果存在M>0，对于一切属于区间X上的x，恒有|f（x）|≤M，则称f（x）在区间X上有界，否则称f（x）在区间上无界。

       2、单调性

       设函数f（x）的定义域为D，区间I包含于D。如果对于区间上任意两点x1及x2，当x1<x2时，恒有f（x1）<f（x2），则称函数f（x）在区间I上是单调递增的；如果对于区间I上任意两点x1及x2，当x1<x2时，恒有f（x1）>f（x2），则称函数f（x）在区间I上是单调递减的。单调递增和单调递减的函数统称为单调函数。

       func应该代表的是function这个英文单词，因为函数的英文是function，所以教材中自定义函数的名称一般用f,fun,func。只是一个名称，为了便于记忆而已。

       function，英语单词，主要用作为名词、动词，作名词时译为“功能；[数]函数；职责；盛大的集会”，作动词时译为“运行；活动；行使职责”。

双语例句：

       1、Do you mind telling me how to use this function? --- No, not at all.

       你介意告诉我怎样使用这个功能吗？不，我一点儿也不介意。

       2、In this case, you have only one operation and, therefore, only one function.

       在这里，您只有一个操作，因此也只有一个函数。

       3、But what if we need to break up our implementation into more than one function?

       但是如果我们需要分解我们的实现代码为多个函数该怎么办？

       好了，今天关于“function”的话题就到这里了。希望大家能够通过我的讲解对“function”有更全面、深入的了解，并且能够在今后的生活中更好地运用所学知识。